[最も好ましい] 円の面積 ��用 101503-円の面積 応用 解���方

円の面積 応用1の解説 春日井市高蔵寺の学習塾 西村セミナールーム

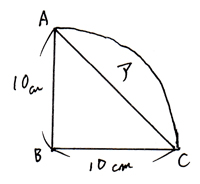
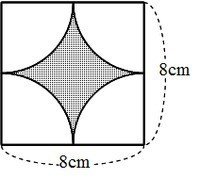
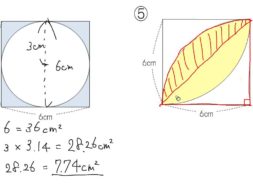
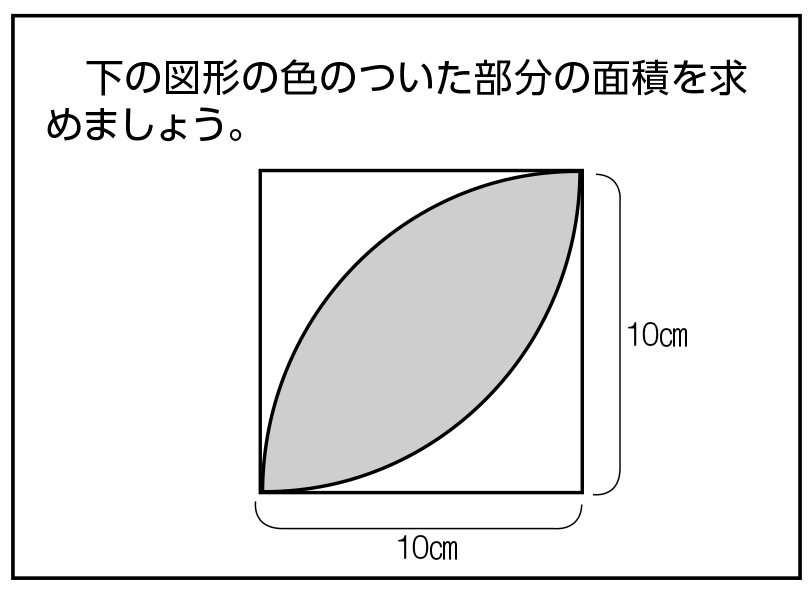
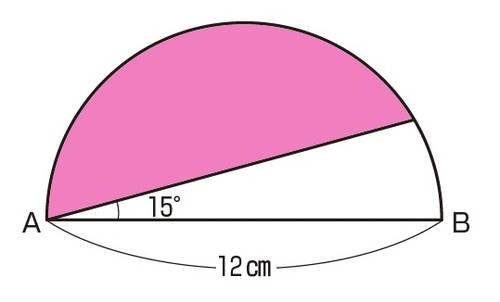
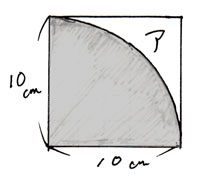
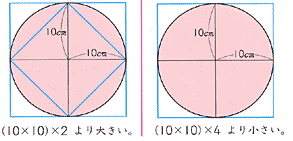
 図形と計量｜正弦定理・余弦定理、面積への応用について 数学1 今回は、正弦定理や余弦定理の図形への応用を学習しましょう。 三角比を扱った総合問題です。 総合問題になると、三角形はもちろん、四角形や円とも絡めた問題も出題されます 57cm²という結果は、正方形の面積100cm²の57％にあたります（正方形の面積の057倍）。 つまり、葉っぱ型の図形の面積は （1辺の長さ）×（1辺の長さ）×057 でもとめることができるのです。 この公式を覚えておくと、問題を効率よく解くことができます。

円の面積 応用 解き方

円の面積 応用 解き方-ここで、S は円の面積、π は円周率、r は円の半径を表します。 このページの続きでは、この公式の導き方のイメージと、円の面積を求める計算問題の解き方を説明しています。 小学生向けに文字を使わない説明もしているので、ぜひご覧ください。 今回は円の面積の求め方を考えてみます。 円の面積は（半径）×（半径）×314 ですが、これはどのように導かれるのかを説明します。 前回、図形の一部分を切り取ったり，はりつけたりして面積の求めやすい形（長方形など）に変形して面積を求めました。

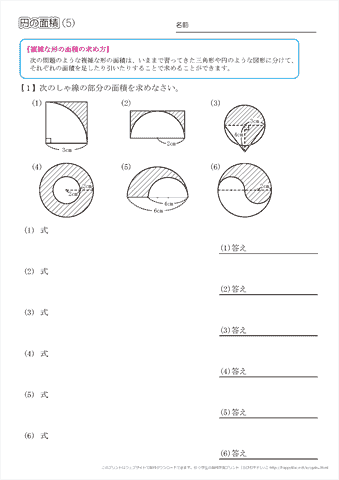
半円を回転させる面積の問題 プリントを使って自分で解こう

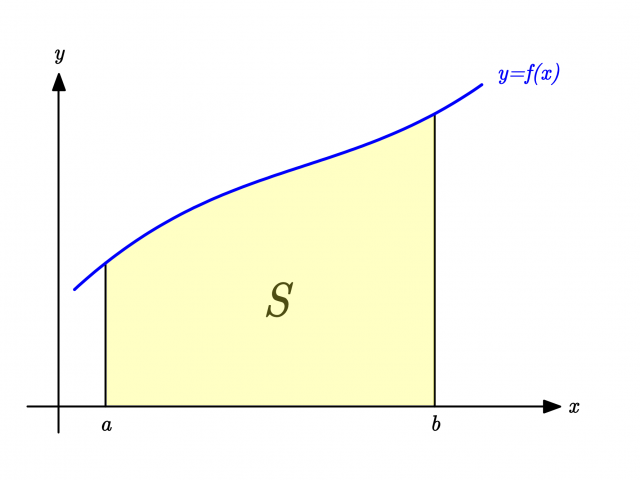
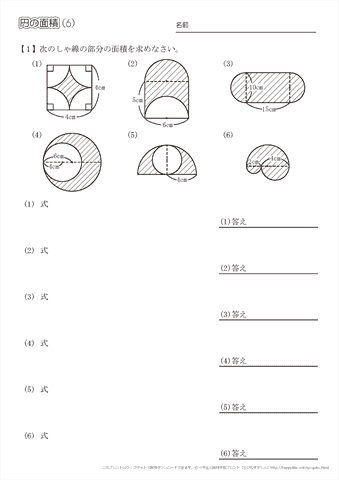
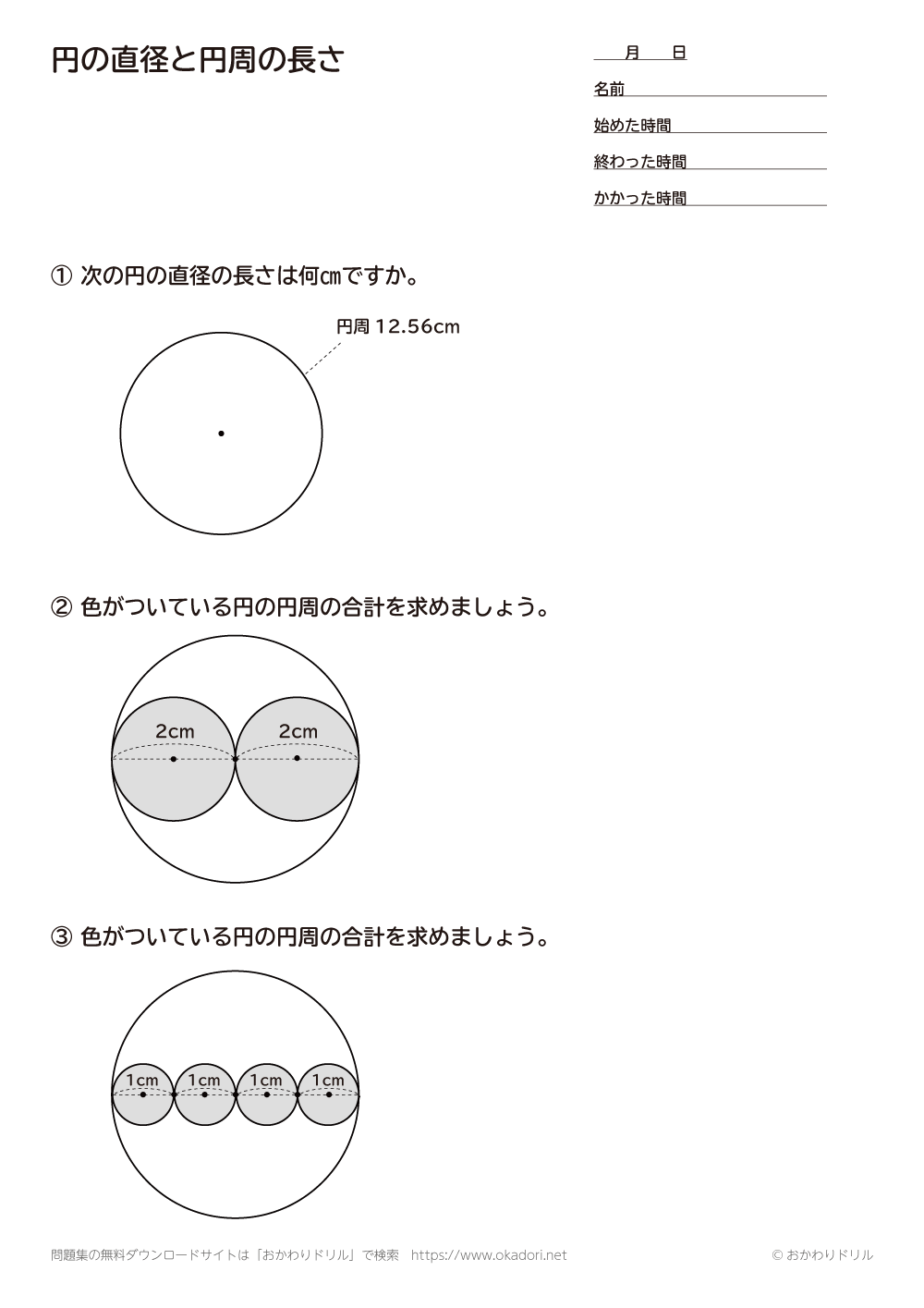
影の部分の面積、周の長さ（4）の解説 面積を求めるには、 おうぎ形から半円を引いてあげればOKですね。 このとき、半円の半径は6㎝になっていることにも注意です。 周の長さは、以下の3つのパーツ（赤、青、緑）を合わせれば求めることができます。101 面積 閉区間 a, b a, b で連続な関数 f(x) f ( x) と， x x 軸，及び2直線 x =a, x =b x = a, x = b とで囲まれる部分の面積は ∫ b a f(x)dx ∫ a b f ( x) d x 例題1 半径 a a の円の面積 S S を求めよ． x2y2 = a2 x 2 y 2 = a 2 を y y について解くと， y ={√a2−x2 (半円の次の問いに答えよ。 半径22cmの円の周の長さを求めよ。 半径12cmの円の面積を求めよ。 直径19cmの円の周の長さを求めよ。 直径15cmの円の面積を求めよ。 次の問いに答えよ。 円周の長さが14πcmの円の面積を求めよ。 円周の長さが8xπcmの円の面積を求めよ。

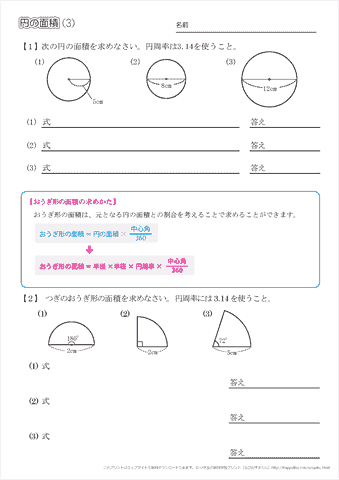
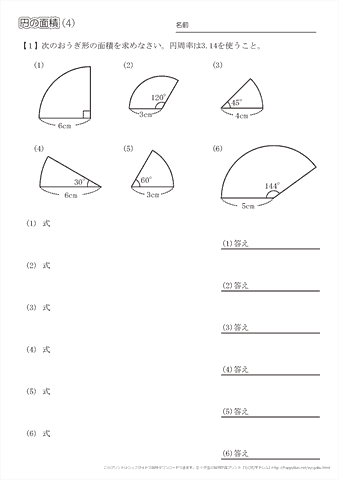
このページは、 小学6年生で習う「円の面積を求める問題集」が無料でダウンロードできる ページです。 ・ 円の面積は「半径×半径×円周率（314）」 という公式を使って求めます。 円の面積が、なぜ「半径×半径×円周率（314）」なのか、もし疑問に思っ 71_円の面積立体の体積1709改訂pdf コメント eboardさんの「円の面積、立体の体積」 1 円の面積 2 円の面積：練習 3 円の面積：練習応用 4 正方形の面積は、 16cm2 16 c m 2 だとすぐにわかりますが、問題はおうぎ形の面積ですね。 面積は、半径×半径×円周率× 1 4 1 4 で求められますが、半径を求めるのは難しそうです。 おうぎ形と正方形の大きさの関係を見ると、正方形の対角線の長さと

円の面積 応用 解き方のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

1	1	1
1	1	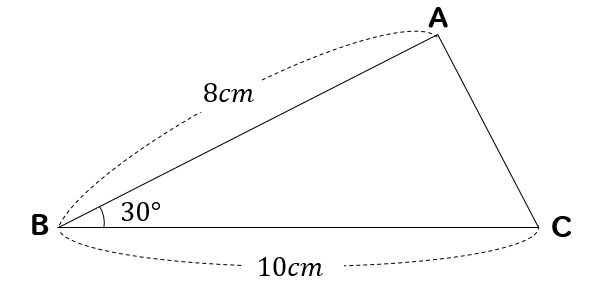1
1	1	1
1	1	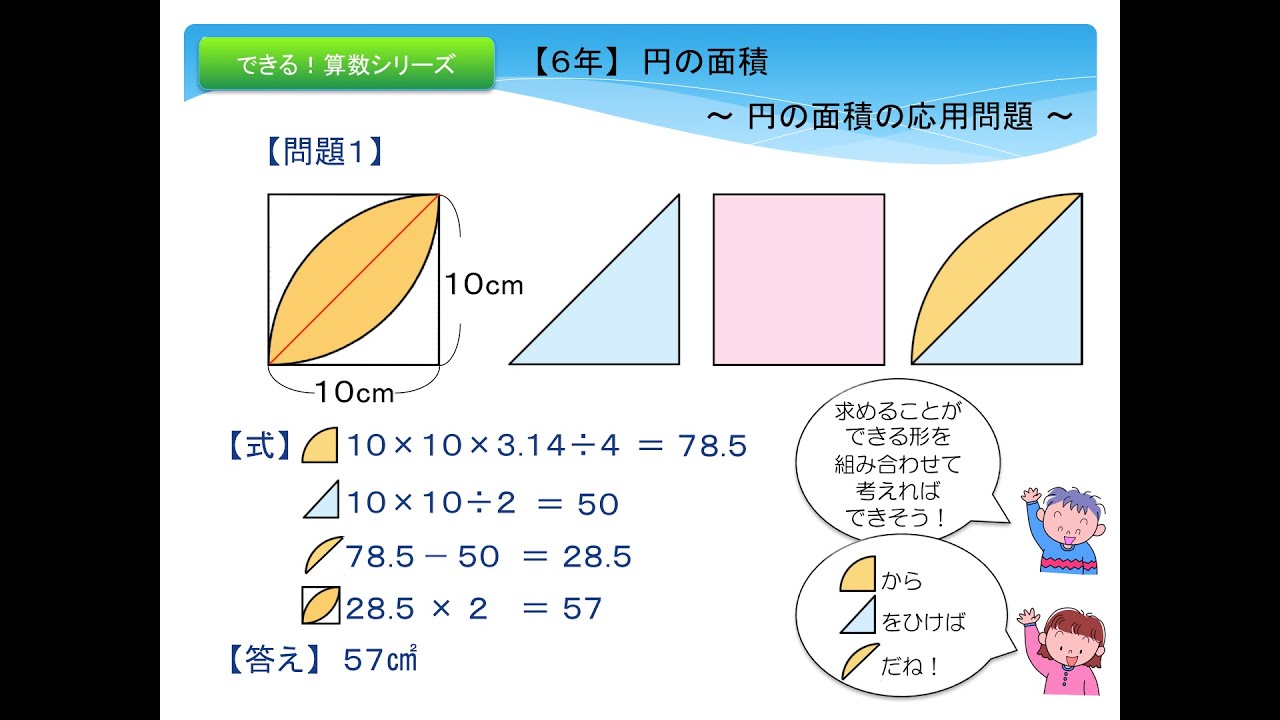1
1	1	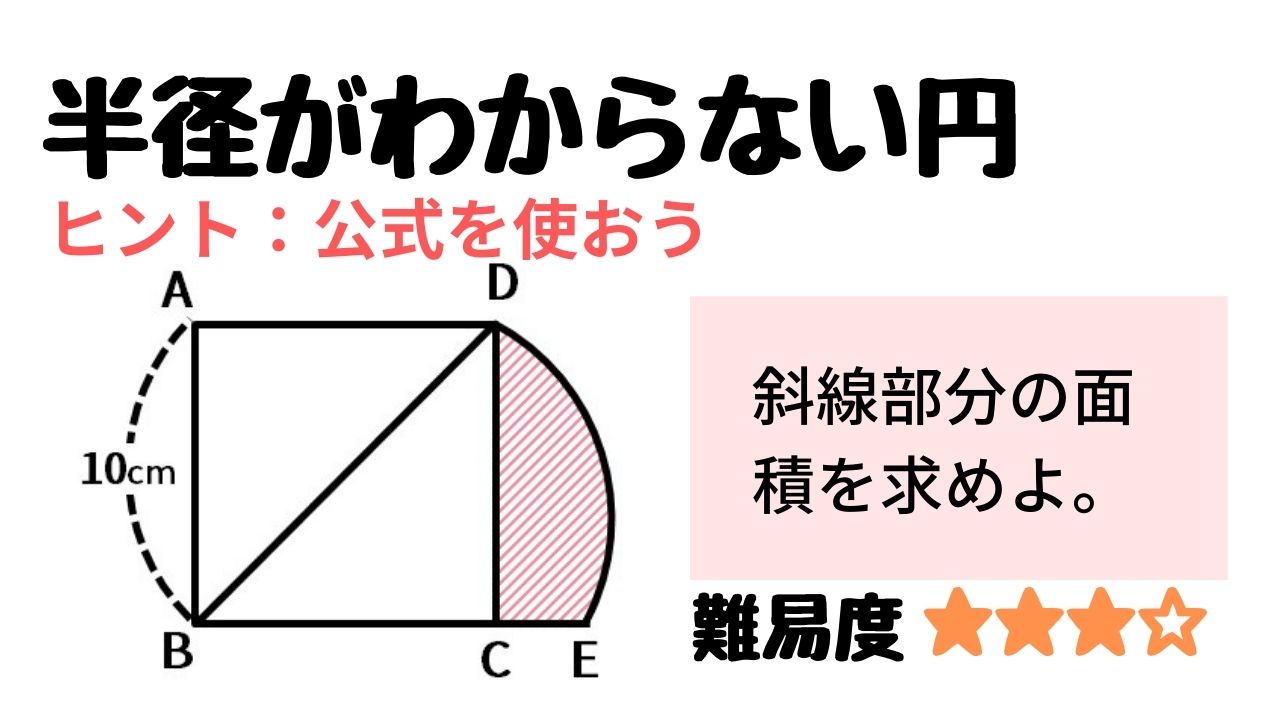1
1	1	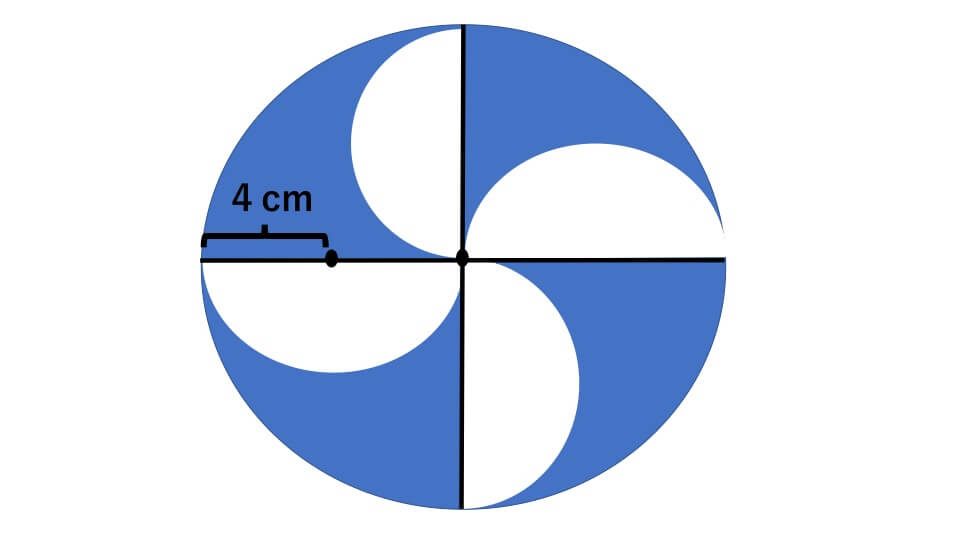1
1	1	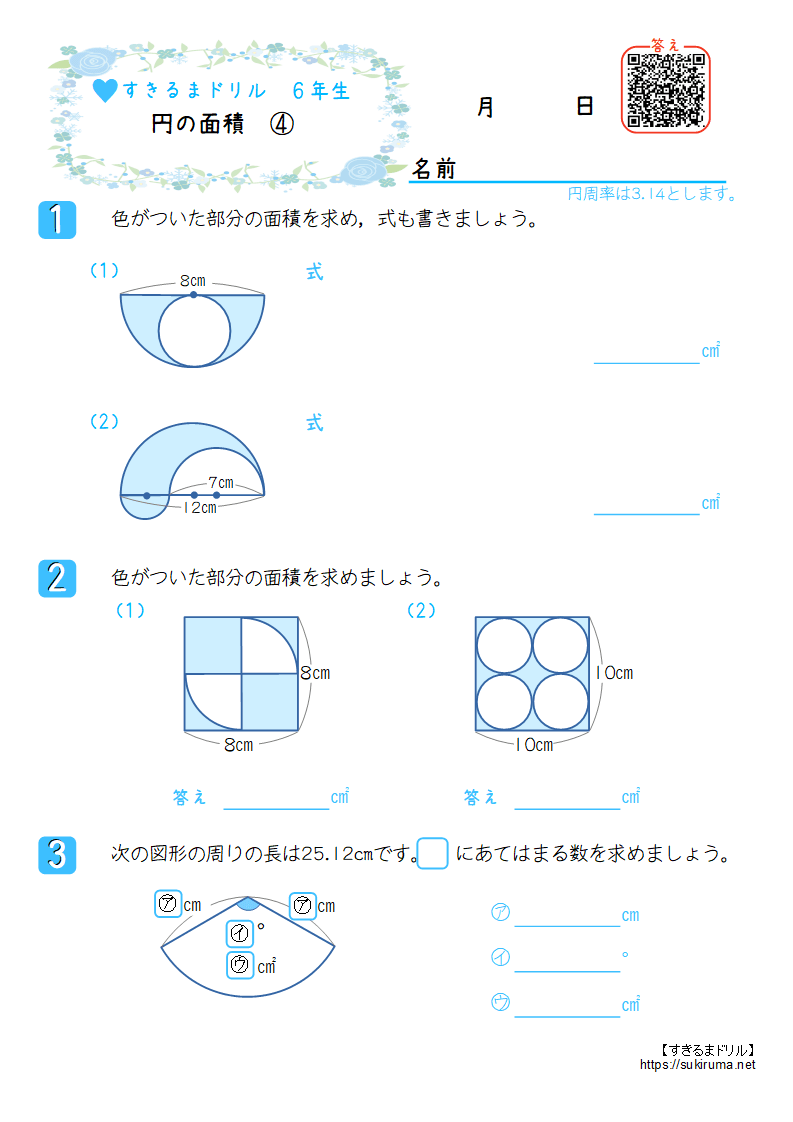1
1	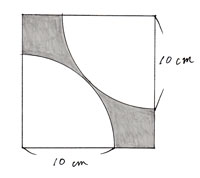1	1
1	1	1
1	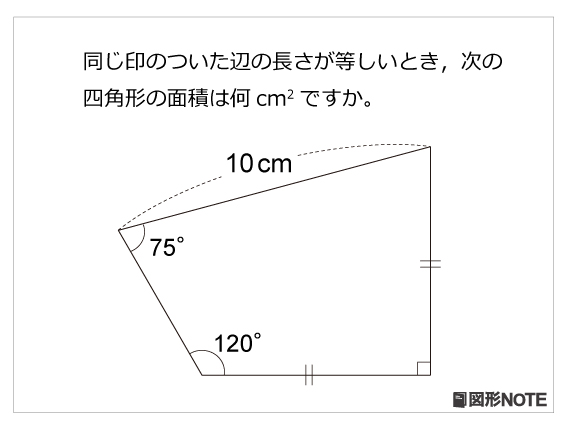1	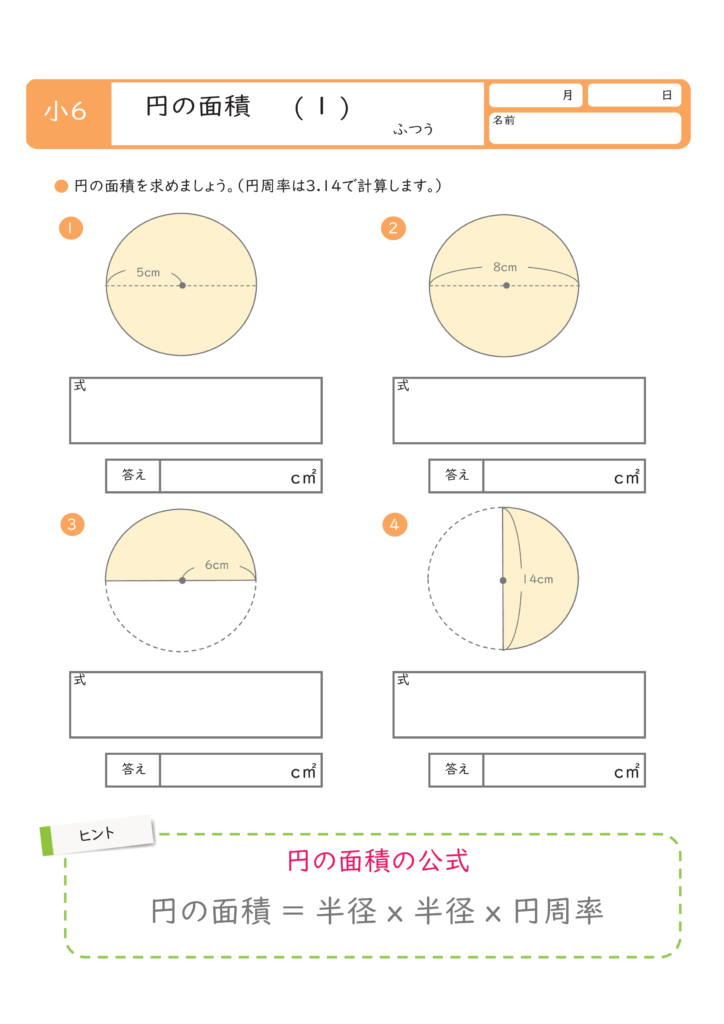1
1	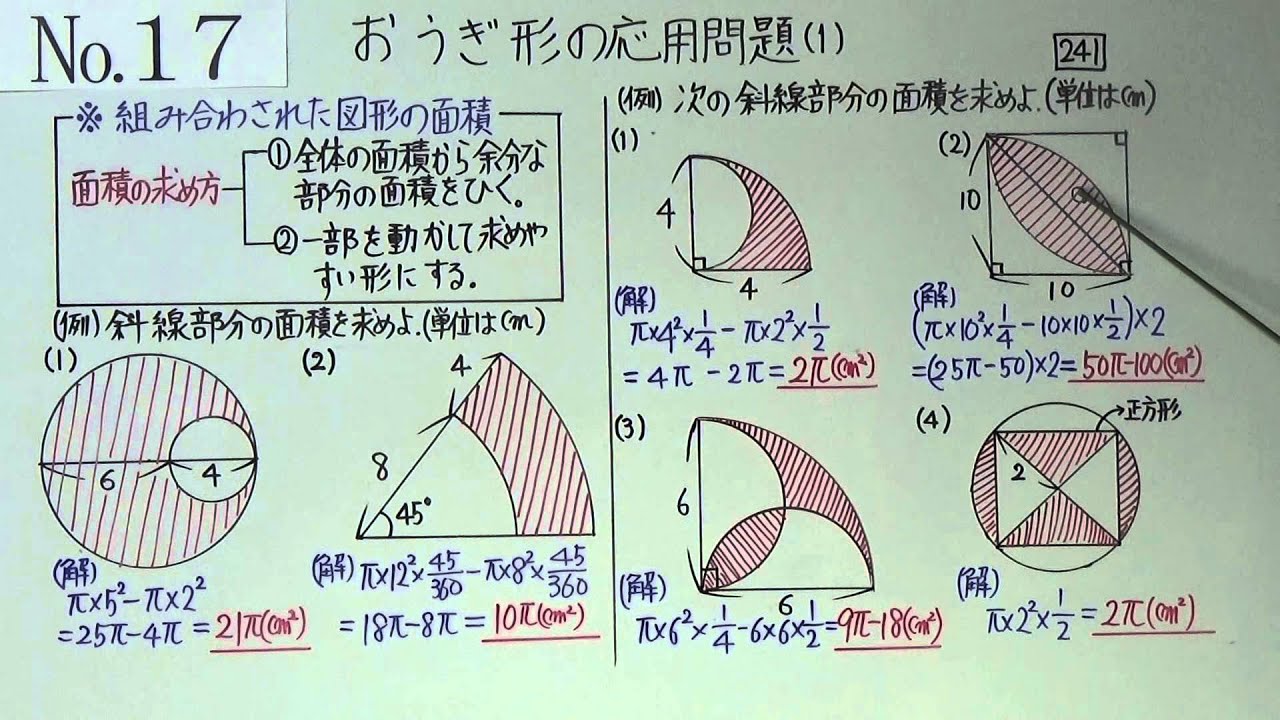1	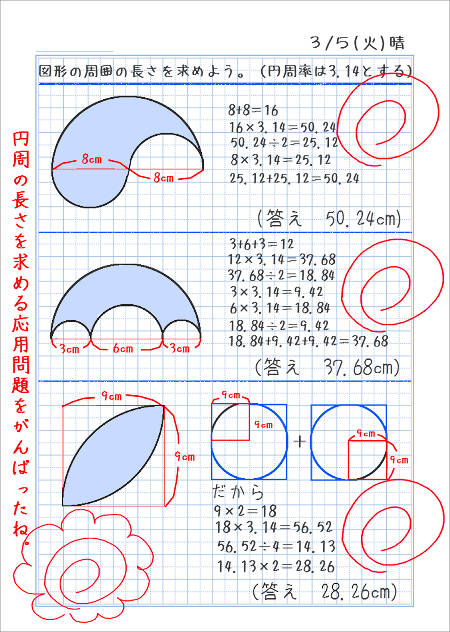1
1	1	1
1	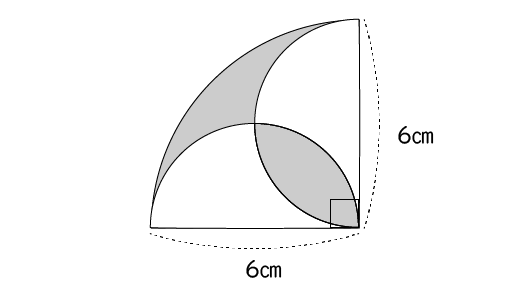1	1
1	1	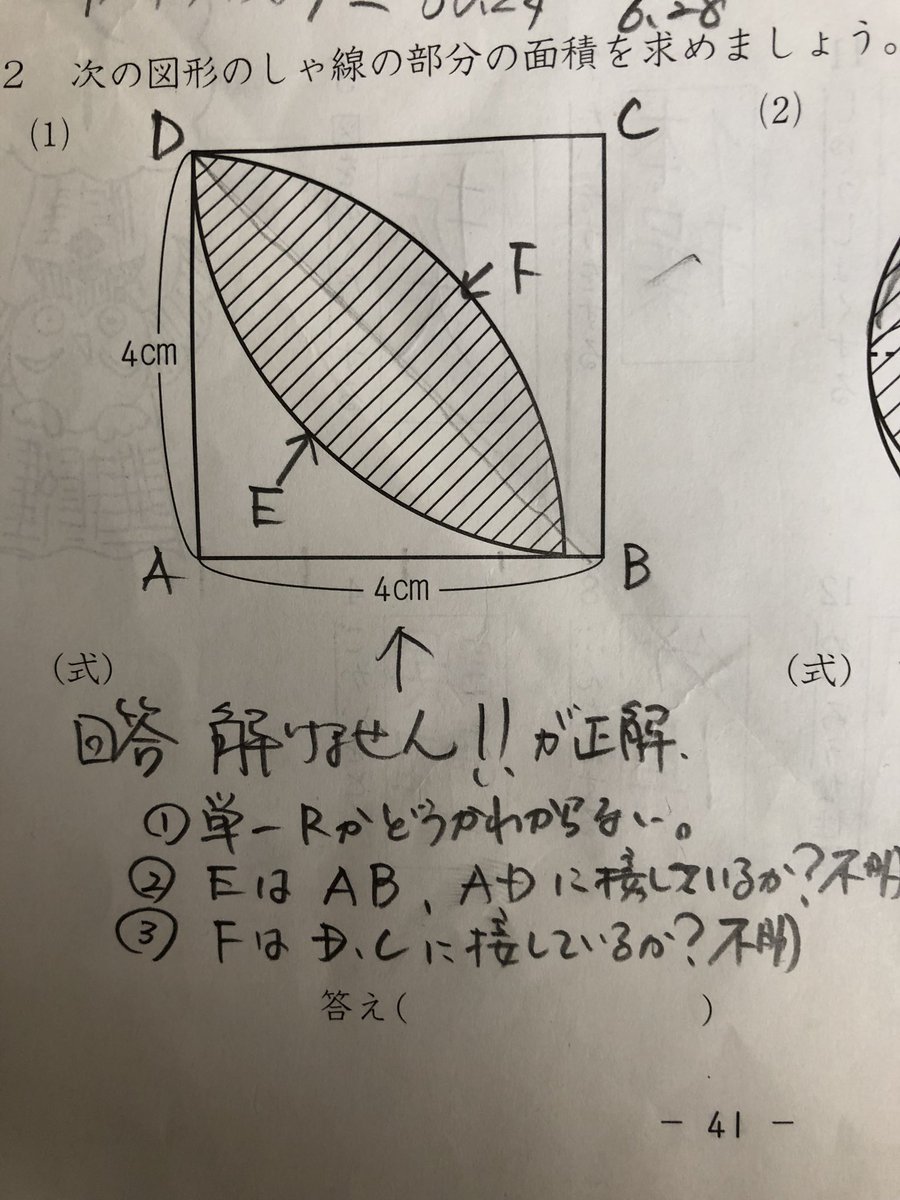1
1	1	1
1	1	1
1	1	1
1	1	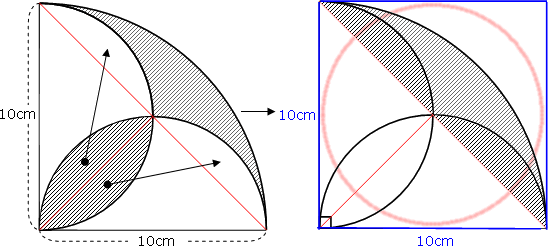1
1	1	1
1	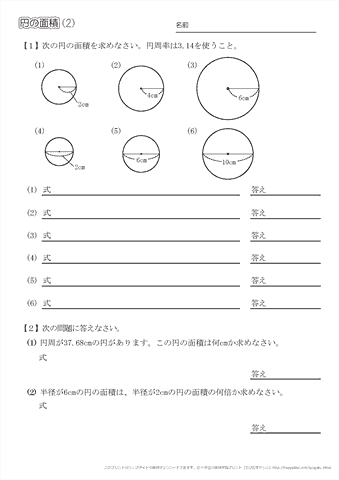1	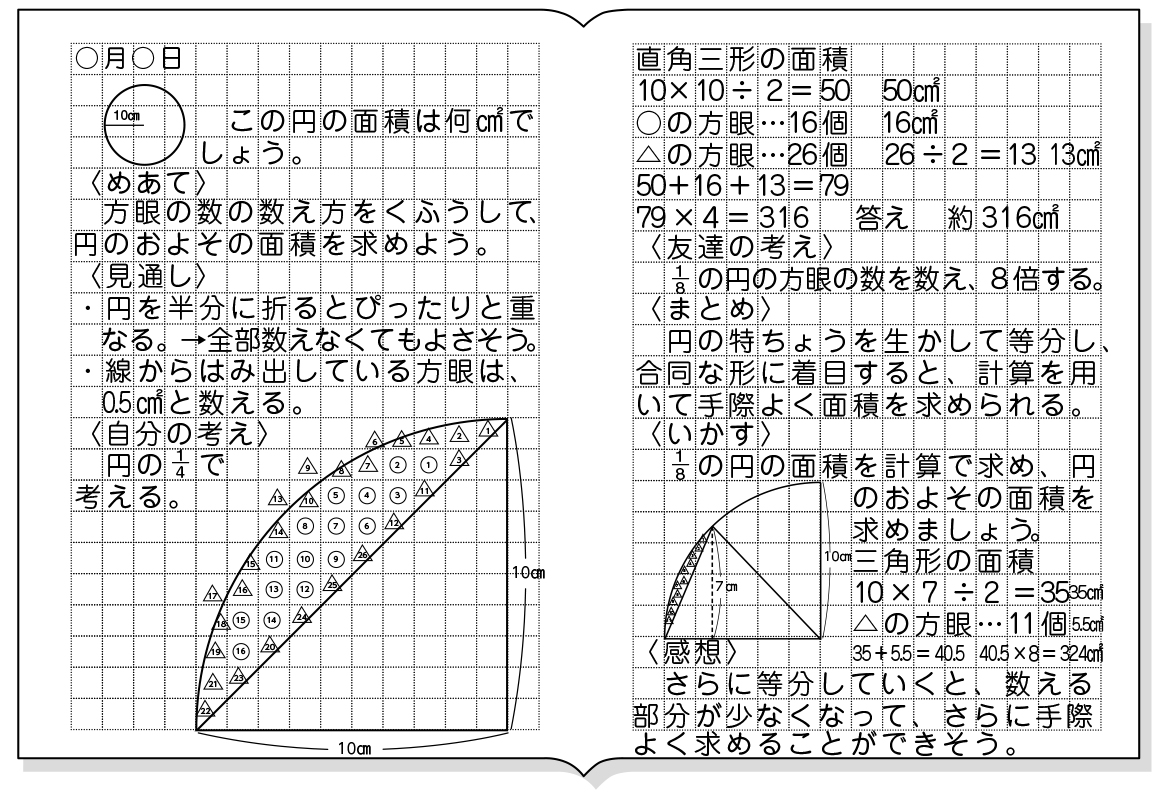1
1	1	1
1	1	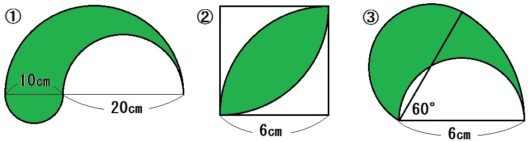1
1	1	1
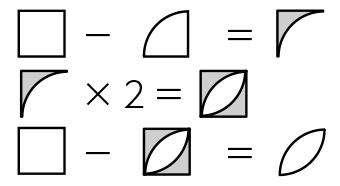1	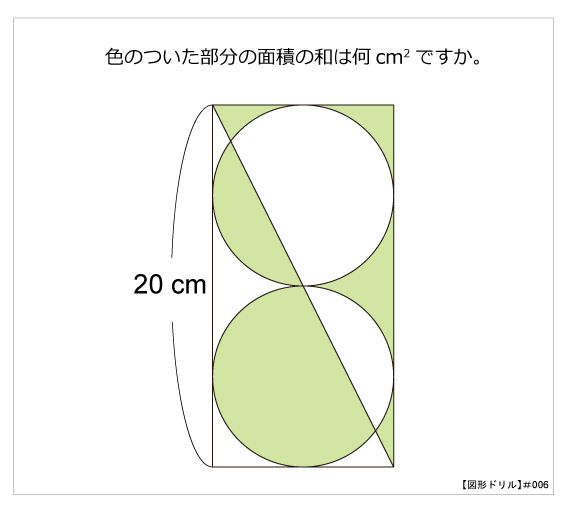1	1
1	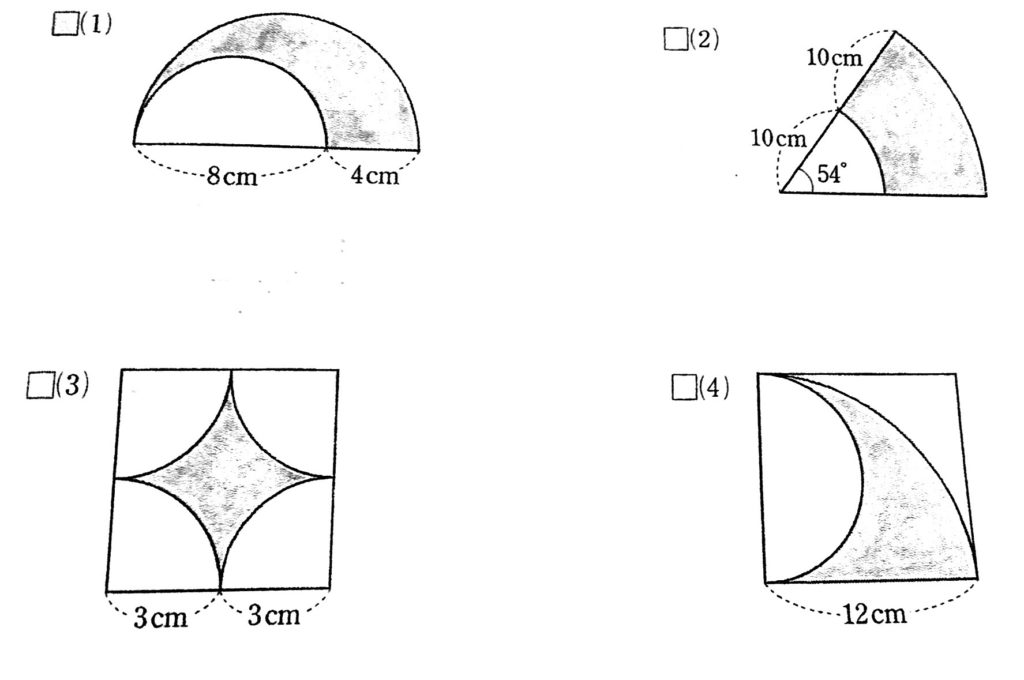1	1
1	1	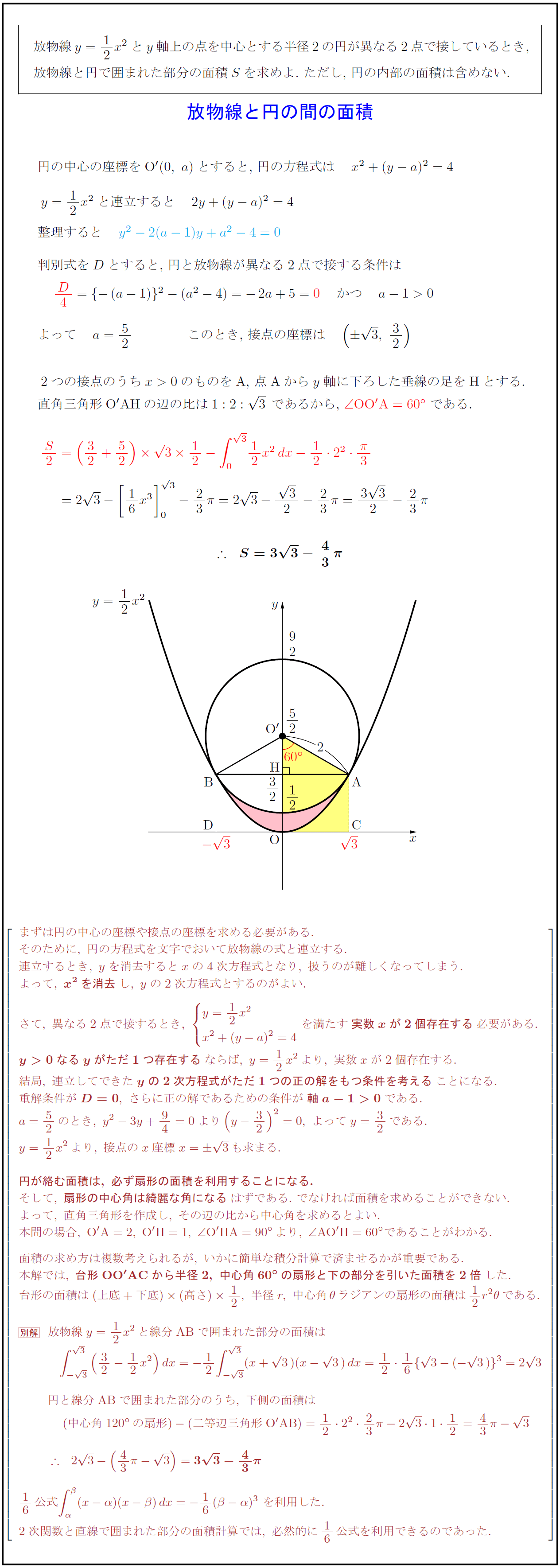1
1	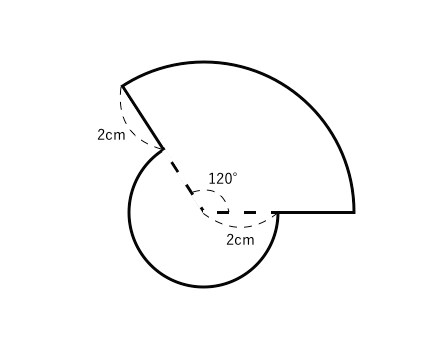1	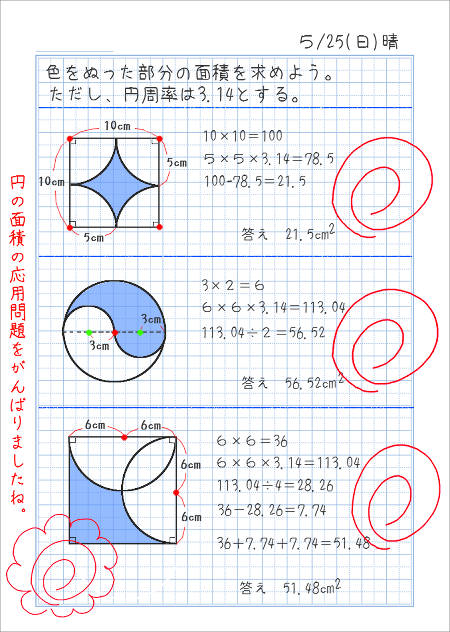1
1	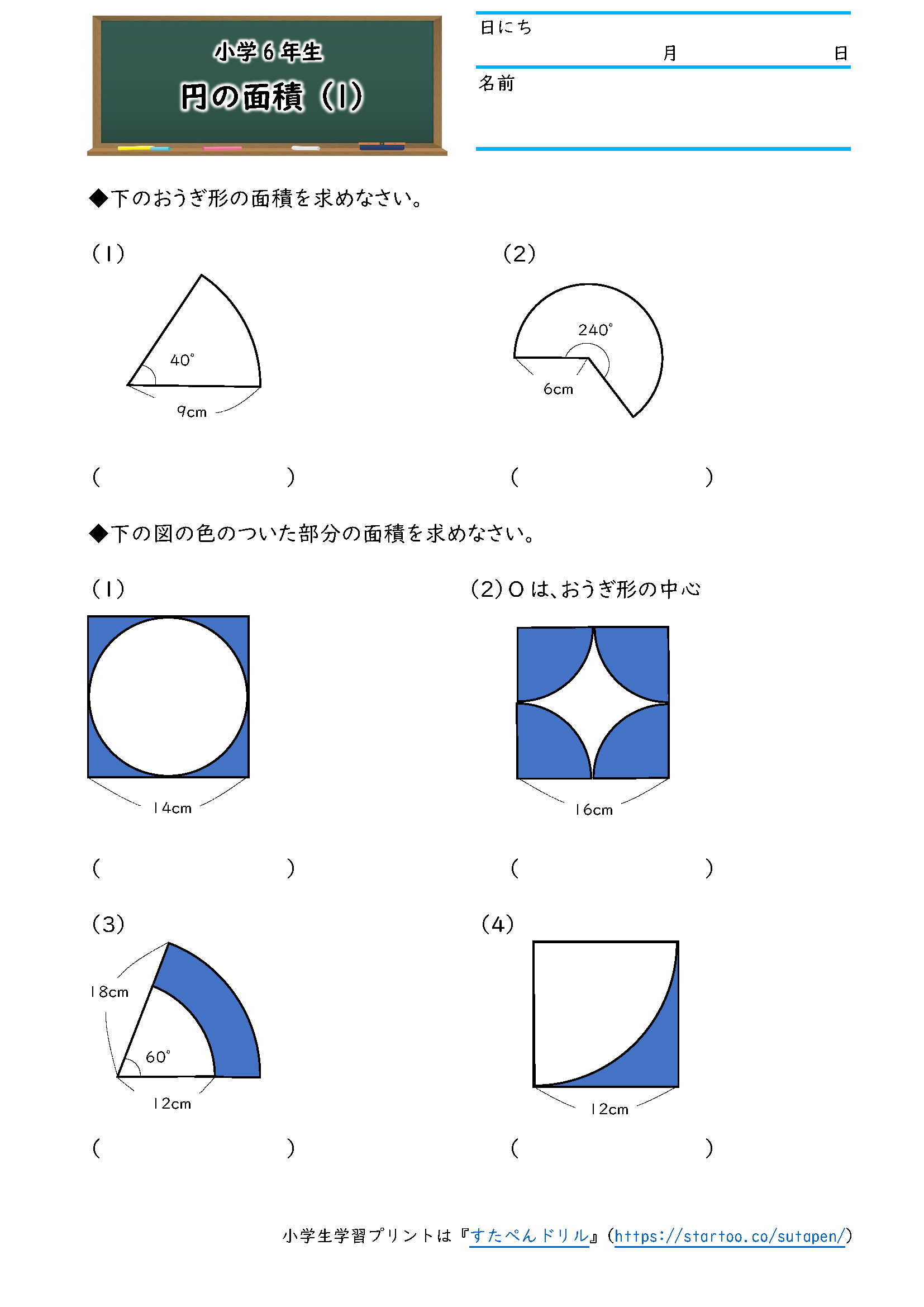1	1
1	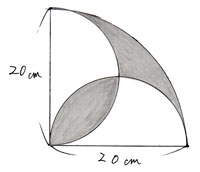1	1
1	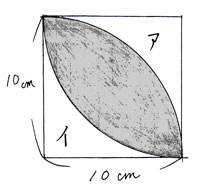1	1
1	1	1
1	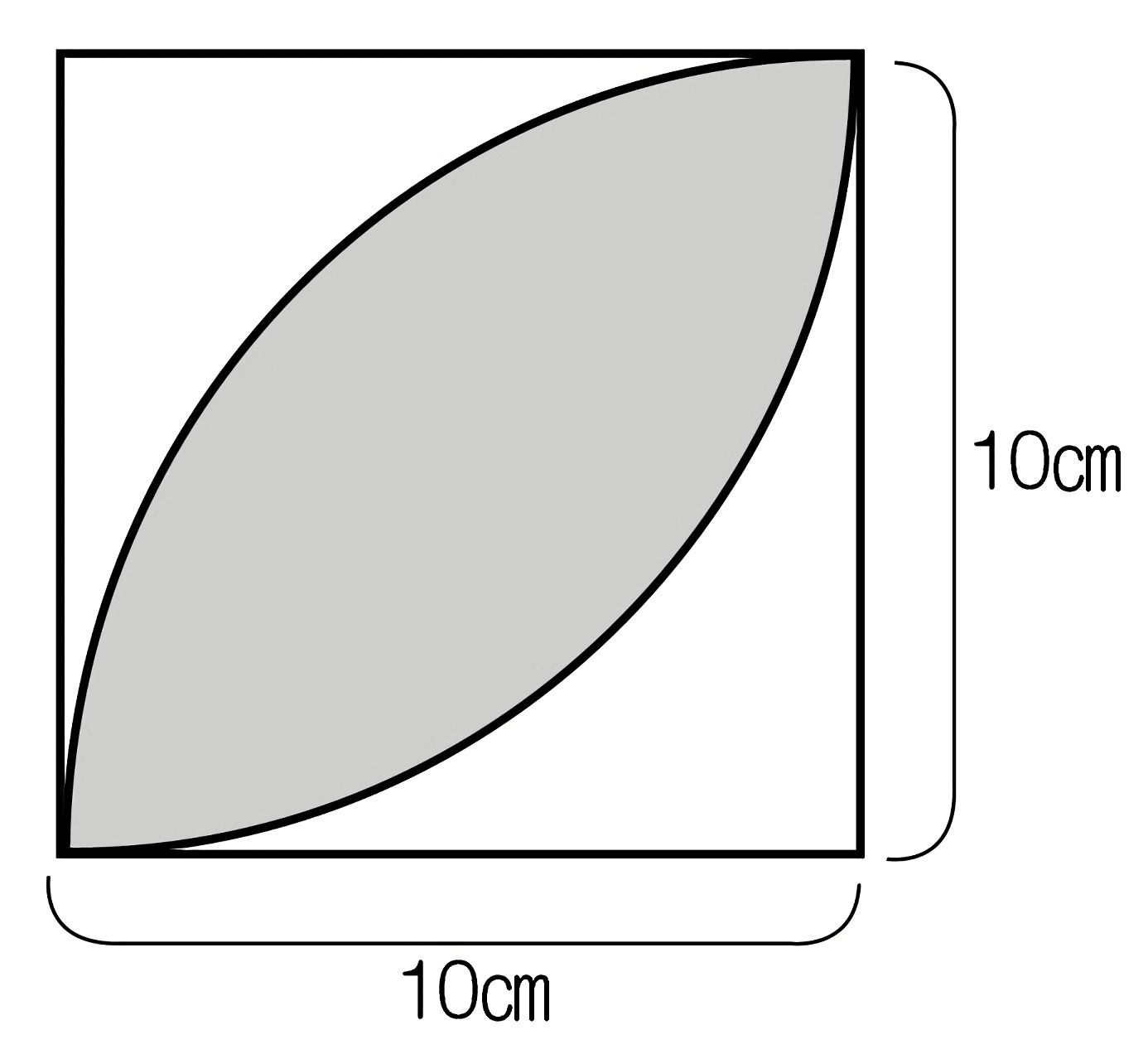1	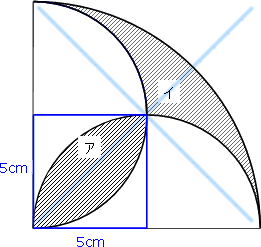1
1	1	1
1	1	1
1	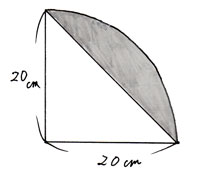1

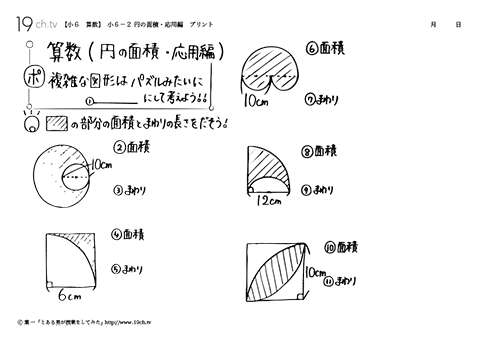
円の面積の求め方を一通り身につけたら、少し応用的な問題にも挑戦してみましょう。 円の面積の応用問題をやってみよう 円の面積の、もっと基本的な問題のノート例はこちらです。 円の面積その1 それでは、小さい円の面積は？大きい円の半径は？（今年 18年 かえつ有明中学） 円の面積は何㎠？（今年 18年 中央大学附属中学） 色部分の面積は？（今年 18年 光塩女子学院中等科） 色のついた部分の

Incoming Term: 円の面積 応用, 円の面積 応用 解き方, 円の面積 応用問題, 円の面積 応用 中学受験, 円の面積 応用 小6, 円の面積 応用 中学, 円の面積 応用 プリント,